Principal-Components Regression

    In my previous post, I have explained multicollinearity and its sources, effect on inference and method of detecting the presences of multicollinearity. Presence of multicollinearity in data may dramatically impact the usefulness of Regression Model. So, now I am going to explain a method for dealing with multicollinearity in regression analysis which is Principal-Components Regression(PCR) . Let's get start it.

Introduction :

    Principal component regression (Massy, 1965; Jolliffe, 1982) is a widely used two-stage procedure: 

1. First performs Principal Component Analysis(PCA) (Pearson,1901; Jolliffe, 2002).
2. Next considers are Regression Model in which the selected principal components are regarded as new regressors. 

However, we should remark that PCA is based only on the regressors, so the principal components are not selected using the information on the response variable. PCR is most popular technique for analyzing multiple regression data that suffer from multicollinearity. PCR is also sometimes used for general dimension reduction. 

Assumption :

1. Linearity of the phenomenon measured.
2. Constant variance of the error terms.
3. Independence of the error terms.
4. Normality of the error term distribution.

Details of the method :

Data representation:

Following centering the standard Gauss-markov linear regression model for y on X can be represented as,

                                        

Where,

             denote the vector of response variable,

             denote the corresponding data matrix of predictor variables.

             : Sample size 

             : predictor variables, with .

Each of the 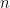rows of denotes one set of observation for the dimensional predictor variables and the respective entry of 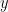denotes the corresponding response variable.

Consider the canonical form of the model

                                        

Where,

            

is a diagonal matrix of the eigenvalues of and is a orthogonal matrix whose columns are the eigenvectors associated with The columns of 

, which define a new set of orthogonal regressors, such as 

                                        

are referred to as principal components. 

Fitting of PCR for the Acetylene Data using Python :

    I am going to use same dataset for Regression Analysis which I have used in my Multicollinearity : Introduction, Sources, Effect and Diagnostics blog

Example : The acetylene Data

Table 1

Table 1 present data concerning the percentage of conversion of 'n-heptane to acetylene' and three explanatory variables(predictor variables or predictors) 'Reactor Temperature (oC)', 'Ratio of H2 to n-Heptane ( mole ratio)' and 'Contact Time (sec)'. 

Step 1: Performs Principal Component Analysis(PCA) on explanatory variable

Import libraries and read data from csv

Check correlation between explanatory variables

Here, we can see that correlation present between explanatory variables. So let's do further regression analysis using PCA. Before calculating PCA, we need to bring all explanatory variables into same unit as they are having different unit. I am going to use StandardScaler() for scaling. 

Explained Variance : The explained variance tells you how much information (variance) can be attributed to each of the principal components. This is important as while you can covert high dimensional space to two dimensional space (Data Reduction), you lose some of the information when you do this. 

Now, we are having three principal component as having three explanatory variables. You can see that the first principal component contains 68.66% of the variance and second principal component contains 29.95% of the variance. Together, the two components contain 98.61% of the information. Therefore, I am going to used first two principal components which are contain maximum information of explanatory variables. We can select any number of principal components according to your data, features and variance that explained by PCA, such that we can achieve high accuracy through model which is good for prediction. 

Source : https://images.app.goo.gl/WBQWbis6vsBLDi2e8

Step 2: Regression Model (selected principal components are regarded as new regressors)

Here, we can see that coefficient of determination is 0.90616 which is good accuracy measure in regression analysis. Coefficient of determination telling us that, how much variation is explaining this model. 

Conclusion : 

Our PCR model can explaining 90.61% variability in the whole data using first two principal components, just 9.39% information is unexplainable in this model, there might be some error's contribution in unexplainable information as accuracy never ever be 100% in statistics (error always be there), which is good for prediction. 

Advantages:

1. PCR can perform regression when the explanatory variables are highly correlated or even collinear.
2. PCR is intuitive : We replace the basis with an orthogonal basis of principal components, drop the components that do not explain much variance, and regress the response onto the remaining components.
3. PCR is automatic : The only decision you need to make is how many principal components to keep
4. We can run PCR when there are more variables than observations(wide data)

Disadvantages : 

1. PCR does not consider the response variable when deciding which principal components to drop. The decision to drop components is based only on the magnitude of the variance of the components. 
2. There is no a priori reason to believe that the principle components that best predict the response

Endnote :

    PCR is a technique for computing regression when the explanatory variable are highly correlated. If has several advantages, but the main drawback of PCR is that the decision about how many principal to keep does not depend on the response variable. Consequently, some of the variables that you keep might not be strong predictors of the response, and some of the components that you drop might be excellent predictors. A good alternatives are Ridge Regression and Partial Least Squares(PLS) Regression.

---Thank you---

Multicollinearity : Introduction, Sources, Effect and Diagnostics

    Regression model are used for a wide variety of applications. A serious problem that may dramatically impact the usefulness of regression model is multicollinearity. So in this post, we will examine the sources of multicollinearity, some of its specific effect on inference and some methods of detecting the presences of multicollinearity.

Introduction :

    In multiple regression, the use and interpretation of model depends on the estimates of the individual regression coefficients either explicitly or implicitly. 

Some examples of inferences :

• Identifying the relative effects of the regressors/predictor variables
• Prediction and/or estimation
• Features(Variables) selection

We write the multiple regression model as 

where  is an  vector of responses, the parameter , are called regression coefficients,   are predictor variables, is no. of records and is no. of predictor variables in model. 

    If there is no linear relationship between the regressors, then inferences such as those illustrated above can be made relatively easily. Where there are near-linear dependencies among the regressors, the problem of multicollinearity is said to exist.  In other words, multicollinearity generally occurs when there are high correlations between two or more regressors. 

Following figure display correlation between predictor variables and . So, we can say that, both predictor are collinear to each other, that mean collinearity present between them.

https://econtutorials.com/blog/difference-perfect-imperfect-multicollinearity/

There are two basic kinds of multicollinearity :

• Structural multicollinearity: This type occurs when we create a new predictor variable using other predictor variable. In other words, caused by you, the analyst, creating new predictor variables. For example, if you create new predictor variable ,  square of the already existed predictor variable , clearly there is a correlation between and .

• Data multicollinearity: This type of multicollinearity is present in the data itself rather than being any artifact of our model. Observational experiments are more likely to display this kind of multicollinearity.

Sources of multicollinearity :

• Insufficient data, In some cases, collecting more data can resolve the issue.
• Dummy variable may be incorrectly used. For example analyst may fail to exclude one category, or add a dummy variable for every category ( e.g. spring, summer, autumn, winter)
• Including a variable in the regression that is actually a combination of two other variables. For example, including “total investment income” when total investment income = income from stocks and bonds + income from savings interest.
• Including two identical (or almost identical) variables. For example, investment income and savings/bond income.
• An overdefined model has more predictor variable than records. 

Effects of multicollinearity :

    Moderate multicollinearity may not be problematic. However, severe multicollinearity is a problem because it can increase the variance of the coefficient estimates and make the estimates very sensitive to minor changes in the model. The result is that the coefficient estimates are unstable and difficult to interpret. following figure is just example for understanding of the variance of the regression coefficients  and its estimates  in situation of multicollinearity.

 

Multicollinearity reduce the statistical power of the analysis, can cause the coefficients to switch signs, and makes it more difficult to specify the correct model.

Multicollinearity Diagnostics :

    There are several techniques have been proposed for detecting multicollinearity, two of them are given as follows :

1. Examination of the Correlation Matrix 
2. Variance Inflation Factors

We will now discuss an illustrate these diagnostics measures.

Examination of the Correlation Matrix :

    A very simple measure of multicollinearity is inspection of the off-diagonal elements in . If the and  are nearly linearly dependent, then will be near unity. 

    The examining the simple correlation between the predictor variables is helpful in detecting near linear dependencies between pair of predictor variables only.  

Variance Inflation Factors :

    The Variance Inflation Factor (VIF) is a measure of collinearity among predictor variables within a multiple regression. It is calculated by taking the the ratio of the variance of all a given model's betas divide by the variance of a single beta if it were fit alone. 

 

Where   is the coefficient determination obtained when is regressed on the remaining predictors. 

    The VIF for each term in the model measures that combine effect of the dependencies among the predictors(regressors) on the variance of that term. One or more large VIFs indicates multicollinearity. Practical experience indicates that if any of the VIFs exceed 5 or 10, it is an indication that the associated regression coefficients are poorly estimated because of multicollinearity. 

Example : The acetylene Data.

Table 1

Table 1 present data concerning the percentage of conversion of 'n-heptane to acetylene' and three explanatory variables(predictor variables or predictors) 'Reactor Temperature (^oC)', 'Ratio of H₂ to n-Heptane ( mole ratio)' and 'Contact Time (sec)'. 

Detecting multicollinearity using Examination of the Correlation Matrix approach :

From the correlation matrix, we can see that the correlation between Reactor Temperature (^oC) and Contact Time (sec) is very high, both predictors are collinear to each other, indicating collinearity in data. 

Detecting multicollinearity using Variance Inflation Factors approach :

    

Here, first two values of VIF for Reactor Temperature and Ratio of H₂ to n-Heptane exceed 5, indicating that that the multicollinearity exist in the data. 

Endnote :

Other techniques for detecting multicollinearity :

1. Eigensystem Analysis of  
2. The Condition Indices
3. The Determinant  of 
4. The F statistic for significance of regression and the individual t (or partial F) statistics
5. The sign and magnitudes of the regression

Methods for dealing with multicollinearity :

1. Collecting Additional Data
2. Model Respecification 
3. Ridge Regression
4. Principal Component Regression 

...