Multicollinearity : Introduction, Sources, Effect and Diagnostics

    Regression model are used for a wide variety of applications. A serious problem that may dramatically impact the usefulness of regression model is multicollinearity. So in this post, we will examine the sources of multicollinearity, some of its specific effect on inference and some methods of detecting the presences of multicollinearity.

Introduction :

    In multiple regression, the use and interpretation of model depends on the estimates of the individual regression coefficients either explicitly or implicitly. 

Some examples of inferences :

• Identifying the relative effects of the regressors/predictor variables
• Prediction and/or estimation
• Features(Variables) selection

We write the multiple regression model as 

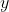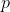where  is an  vector of responses, the parameter , are called regression coefficients,   are predictor variables, is no. of records and is no. of predictor variables in model. 

    If there is no linear relationship between the regressors, then inferences such as those illustrated above can be made relatively easily. Where there are near-linear dependencies among the regressors, the problem of multicollinearity is said to exist.  In other words, multicollinearity generally occurs when there are high correlations between two or more regressors. 

Following figure display correlation between predictor variables 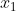and 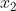. So, we can say that, both predictor are collinear to each other, that mean collinearity present between them.

https://econtutorials.com/blog/difference-perfect-imperfect-multicollinearity/

There are two basic kinds of multicollinearity :

• Structural multicollinearity: This type occurs when we create a new predictor variable using other predictor variable. In other words, caused by you, the analyst, creating new predictor variables. For example, if you create new predictor variable ,  square of the already existed predictor variable , clearly there is a correlation between and .

• Data multicollinearity: This type of multicollinearity is present in the data itself rather than being any artifact of our model. Observational experiments are more likely to display this kind of multicollinearity.

Sources of multicollinearity :

• Insufficient data, In some cases, collecting more data can resolve the issue.
• Dummy variable may be incorrectly used. For example analyst may fail to exclude one category, or add a dummy variable for every category ( e.g. spring, summer, autumn, winter)
• Including a variable in the regression that is actually a combination of two other variables. For example, including “total investment income” when total investment income = income from stocks and bonds + income from savings interest.
• Including two identical (or almost identical) variables. For example, investment income and savings/bond income.
• An overdefined model has more predictor variable than records. 

Effects of multicollinearity :

    Moderate multicollinearity may not be problematic. However, severe multicollinearity is a problem because it can increase the variance of the coefficient estimates and make the estimates very sensitive to minor changes in the model. The result is that the coefficient estimates are unstable and difficult to interpret. following figure is just example for understanding of the variance of the regression coefficients  and its estimates  in situation of multicollinearity.

 

Multicollinearity reduce the statistical power of the analysis, can cause the coefficients to switch signs, and makes it more difficult to specify the correct model.

Multicollinearity Diagnostics :

    There are several techniques have been proposed for detecting multicollinearity, two of them are given as follows :

1. Examination of the Correlation Matrix 
2. Variance Inflation Factors

We will now discuss an illustrate these diagnostics measures.

Examination of the Correlation Matrix :

    A very simple measure of multicollinearity is inspection of the off-diagonal elements in . If the and  are nearly linearly dependent, then will be near unity. 

    The examining the simple correlation between the predictor variables is helpful in detecting near linear dependencies between pair of predictor variables only.  

Variance Inflation Factors :

    The Variance Inflation Factor (VIF) is a measure of collinearity among predictor variables within a multiple regression. It is calculated by taking the the ratio of the variance of all a given model's betas divide by the variance of a single beta if it were fit alone. 

 

Where   is the coefficient determination obtained when is regressed on the remaining predictors. 

    The VIF for each term in the model measures that combine effect of the dependencies among the predictors(regressors) on the variance of that term. One or more large VIFs indicates multicollinearity. Practical experience indicates that if any of the VIFs exceed 5 or 10, it is an indication that the associated regression coefficients are poorly estimated because of multicollinearity. 

Example : The acetylene Data.

Table 1

Table 1 present data concerning the percentage of conversion of 'n-heptane to acetylene' and three explanatory variables(predictor variables or predictors) 'Reactor Temperature (^oC)', 'Ratio of H₂ to n-Heptane ( mole ratio)' and 'Contact Time (sec)'. 

Detecting multicollinearity using Examination of the Correlation Matrix approach :

From the correlation matrix, we can see that the correlation between Reactor Temperature (^oC) and Contact Time (sec) is very high, both predictors are collinear to each other, indicating collinearity in data. 

Detecting multicollinearity using Variance Inflation Factors approach :

    

Here, first two values of VIF for Reactor Temperature and Ratio of H₂ to n-Heptane exceed 5, indicating that that the multicollinearity exist in the data. 

Endnote :

Other techniques for detecting multicollinearity :

1. Eigensystem Analysis of  
2. The Condition Indices
3. The Determinant  of 
4. The F statistic for significance of regression and the individual t (or partial F) statistics
5. The sign and magnitudes of the regression

Methods for dealing with multicollinearity :

1. Collecting Additional Data
2. Model Respecification 
3. Ridge Regression
4. Principal Component Regression 

...